Serverless Architectures
Serverless architectures are application designs that incorporate third-party “Backend as a Service” (BaaS) services, and/or that include custom code run in managed, ephemeral containers on a “Functions as a Service” (FaaS) platform. By using these ideas, and related ones like single-page applications, such architectures remove much of the need for a traditional always-on server component. Serverless architectures may benefit from significantly reduced operational cost, complexity, and engineering lead time, at a cost of increased reliance on vendor dependencies and comparatively immature supporting services.
22 May 2018
Contents
- What is Serverless?
- Benefits
- Drawbacks
- The Future of Serverless
- Conclusion
Sidebars
Serverless computing, or more simply Serverless, is a hot topic in the software architecture world. The “Big Three” cloud vendors—Amazon, Google, and Microsoft—are heavily invested in Serverless, and we’ve seen plenty of books, open-source projects, conferences, and software vendors dedicated to the subject. But what is Serverless, and why is (or isn’t) it worth considering? In this article I hope to enlighten you a little on these questions.
To start we'll look at the “what” of Serverless. We’ll get into the benefits and drawbacks of the approach later.
What is Serverless?
Like many trends in software, there’s no one clear view of what Serverless is. For starters, it encompasses two different but overlapping areas:
- Serverless was first used to describe applications that significantly or fully incorporate third-party, cloud-hosted applications and services, to manage server-side logic and state. These are typically “rich client” applications—think single-page web apps, or mobile apps—that use the vast ecosystem of cloud-accessible databases (e.g., Parse, Firebase), authentication services (e.g., Auth0, AWS Cognito), and so on. These types of services have been previously described as “(Mobile) Backend as a Service", and I use "BaaS" as shorthand in the rest of this article.
- Serverless can also mean applications where server-side logic is still written by the application developer, but, unlike traditional architectures, it’s run in stateless compute containers that are event-triggered, ephemeral (may only last for one invocation), and fully managed by a third party. One way to think of this is “Functions as a Service” or "FaaS". (Note: The original source for this name—a tweet by @marak—is no longer publicly available.) AWS Lambda is one of the most popular implementations of a Functions-as-a-Service platform at present, but there are many others, too.
In this article, we’ll primarily focus on FaaS. Not only is it the area of Serverless that’s newer and driving a lot of the hype, but it has significant differences to how we typically think about technical architecture.
BaaS and FaaS are related in their operational attributes (e.g., no resource management) and are frequently used together. The large cloud vendors all have “Serverless portfolios” that include both BaaS and FaaS products—for example, here’s Amazon’s Serverless product page. Google’s Firebase BaaS database has explicit FaaS support through Google Cloud Functions for Firebase.
There is similar linking of the two areas from smaller companies too. Auth0 started with a BaaS product that implemented many facets of user management, and subsequently created the companion FaaS service Webtask. The company have taken this idea even further with Extend, which enables other SaaS and BaaS companies to easily add a FaaS capability to existing products so they can create a unified Serverless product.
A couple of examples
UI-driven applications
Let’s think about a traditional three-tier client-oriented system with server-side logic. A good example is a typical ecommerce app—dare I say an online pet store?
Traditionally, the architecture will look something like the diagram below. Let’s say it’s implemented in Java or Javascript on the server side, with an HTML + Javascript component as the client:
With this architecture the client can be relatively unintelligent, with much of the logic in the system—authentication, page navigation, searching, transactions—implemented by the server application.
With a Serverless architecture this may end up looking more like this:
This is a massively simplified view, but even here we see a number of significant changes:
- We’ve deleted the authentication logic in the original application and have replaced it with a third-party BaaS service (e.g., Auth0.)
- Using another example of BaaS, we’ve allowed the client direct access to a subset of our database (for product listings), which itself is fully hosted by a third party (e.g., Google Firebase.) We likely have a different security profile for the client accessing the database in this way than for server resources that access the database.
- These previous two points imply a very important third: some logic that was in the Pet Store server is now within the client—e.g., keeping track of a user session, understanding the UX structure of the application, reading from a database and translating that into a usable view, etc. The client is well on its way to becoming a Single Page Application.
- We may want to keep some UX-related functionality in the server, if, for example, it’s compute intensive or requires access to significant amounts of data. In our pet store, an example is “search.” Instead of having an always-running server, as existed in the original architecture, we can instead implement a FaaS function that responds to HTTP requests via an API gateway (described later). Both the client and the server “search” function read from the same database for product data.
- Finally, we may replace our “purchase” functionality with another separate FaaS function, choosing to keep it on the server side for security reasons, rather than reimplement it in the client. It too is fronted by an API gateway. Breaking up different logical requirements into separately deployed components is a very common approach when using FaaS.
If we choose to use AWS Lambda as our FaaS platform we can port the search code from the original Pet Store server to the new Pet Store Search function without a complete rewrite, since Lambda supports Java and Javascript—our original implementation languages.
Stepping back a little, this example demonstrates another very important point about Serverless architectures. In the original version, all flow, control, and security was managed by the central server application. In the Serverless version there is no central arbiter of these concerns. Instead we see a preference for choreography over orchestration, with each component playing a more architecturally aware role—an idea also common in a microservices approach.
There are many benefits to such an approach. As Sam Newman notes in his Building Microservices book, systems built this way are often “more flexible and amenable to change,” both as a whole and through independent updates to components; there is better division of concerns; and there are also some fascinating cost benefits, a point that Gojko Adzic discusses in this excellent talk.
Of course, such a design is a trade-off: it requires better distributed monitoring (more on this later), and we rely more significantly on the security capabilities of the underlying platform. More fundamentally, there are a greater number of moving pieces to get our heads around than there are with the monolithic application we had originally. Whether the benefits of flexibility and cost are worth the added complexity of multiple backend components is very context dependent.
Message-driven applications
A different example is a backend data-processing service.
Say you’re writing a user-centric application that needs to quickly respond to UI requests, and, secondarily, it needs to capture all the different types of user activity that are occurring, for subsequent processing. Think about an online advertisement system: when a user clicks on an ad you want to very quickly redirect them to the target of that ad. At the same time, you need to collect the fact that the click has happened so that you can charge the advertiser. (This example is not hypothetical—my former team at Intent Media had exactly this need, which they implemented in a Serverless way.)
Traditionally, the architecture may look as below. The “Ad Server” synchronously responds to the user (not shown) and also posts a “click message” to a channel. This message is then asynchronously processed by a “click processor” application that updates a database, e.g., to decrement the advertiser’s budget.
In the Serverless world this looks as follows:
Can you see the difference? The change in architecture is much smaller here compared to our first example—this is why asynchronous message processing is a very popular use case for Serverless technologies. We’ve replaced a long-lived message-consumer application with a FaaS function. This function runs within the event-driven context the vendor provides. Note that the cloud platform vendor supplies both the message broker and the FaaS environment—the two systems are closely tied to each other.
The FaaS environment may also process several messages in parallel by instantiating multiple copies of the function code. Depending on how we wrote the original process this may be a new concept we need to consider.
Unpacking "Function as a Service"
We've mentioned FaaS a lot already, but it's time to dig into what it really means. To do this let's look at the opening description for Amazon's FaaS product: Lambda. I've added some tokens to it, which I’ll expand on.
AWS Lambda lets you run code without provisioning or managing servers. (1) ... With Lambda, you can run code for virtually any type of application or backend service (2) - all with zero administration. Just upload your code and Lambda takes care of everything required to run (3) and scale (4) your code with high availability. You can set up your code to automatically trigger from other AWS services (5) or call it directly from any web or mobile app (6).
- Fundamentally, FaaS is about running backend code without managing your own server systems or your own long-lived server applications. That second clause—long-lived server applications—is a key difference when comparing with other modern architectural trends like containers and PaaS (Platform as a Service).
- FaaS offerings do not require coding to a specific framework or library. FaaS functions are regular applications when it comes to language and environment. For instance, AWS Lambda functions can be implemented “first class” in Javascript, Python, Go, any JVM language (Java, Clojure, Scala, etc.), or any .NET language. However your Lambda function can also execute another process that is bundled with its deployment artifact, so you can actually use any language that can compile down to a Unix process (see Apex, later in this article).
- Deployment is very different from traditional systems since we have no server applications to run ourselves. In a FaaS environment we upload the code for our function to the FaaS provider, and the provider does everything else necessary for provisioning resources, instantiating VMs, managing processes, etc.
- Horizontal scaling is completely automatic, elastic, and managed by the provider. If your system needs to be processing 100 requests in parallel the provider will handle that without any extra configuration on your part. The “compute containers” executing your functions are ephemeral, with the FaaS provider creating and destroying them purely driven by runtime need. Most importantly, with FaaS the vendor handles all underlying resource provisioning and allocation—no cluster or VM management is required by the user at all.
- Functions in FaaS are typically triggered by event types defined by the provider. With Amazon AWS such stimuli include S3 (file/object) updates, time (scheduled tasks), and messages added to a message bus (e.g., Kinesis).
- Most providers also allow functions to be triggered as a response to inbound HTTP requests; in AWS one typically enables this by way of using an API gateway. We used an API gateway in our Pet Store example for our “search” and “purchase” functions. Functions can also be invoked directly via a platform-provided API, either externally or from within the same cloud environment, but this is a comparatively uncommon use.
If we go back to our click-processing example from earlier, FaaS replaces the click-processing server (possibly a physical machine, but definitely a specific application) with something that doesn’t need a provisioned server, nor an application that is running all the time.
FaaS functions have significant architectural restrictions though, especially when it comes to state and execution duration. We’ll get to that soon.
Let’s consider our click-processing example again. The only code that needs to change when moving to FaaS is the “main method” (startup) code, in that it is deleted, and likely the specific code that is the top-level message handler (the “message listener interface” implementation), but this might only be a change in method signature. The rest of the code (e.g., the code that writes to the database) is no different in a FaaS world.
Let’s return to our click processor. Say that we were having a good day and customers were clicking on ten times as many ads as usual. For the traditional architecture, would our click-processing application be able to handle this? For example, did we develop our application to be able to handle multiple messages at a time? If we did, would one running instance of the application be enough to process the load? If we are able to run multiple processes, is autoscaling automatic or do we need to reconfigure that manually? With a FaaS approach all of these questions are already answered—you need to write the function ahead of time to assume horizontal-scaled parallelism, but from that point on the FaaS provider automatically handles all scaling needs.
State
FaaS functions have significant restrictions when it comes to local (machine/instance-bound) state—i.e., data that you store in variables in memory, or data that you write to local disk. You do have such storage available, but you have no guarantee that such state is persisted across multiple invocations, and, more strongly, you should not assume that state from one invocation of a function will be available to another invocation of the same function. FaaS functions are therefore often described as stateless, but it’s more accurate to say that any state of a FaaS function that is required to be persistent needs to be externalized outside of the FaaS function instance.
For FaaS functions that are naturally stateless—i.e., those that provide a purely functional transformation of their input to their output—this is of no concern. But for others this can have a large impact on application architecture, albeit not a unique one—the “Twelve-Factor app” concept has precisely the same restriction. Such state-oriented functions will typically make use of a database, a cross-application cache (like Redis), or network file/object store (like S3) to store state across requests, or to provide further input necessary to handle a request.
Execution duration
FaaS functions are typically limited in how long each invocation is allowed to run. At present the “timeout” for an AWS Lambda function to respond to an event is at most five minutes, before being terminated. Microsoft Azure and Google Cloud Functions have similar limits.
This means that certain classes of long-lived tasks are not suited to FaaS functions without re-architecture—you may need to create several different coordinated FaaS functions, whereas in a traditional environment you may have one long-duration task performing both coordination and execution.
Startup latency and “cold starts”
It takes some time for a FaaS platform to initialize an instance of a function before each event. This startup latency can vary significantly, even for one specific function, depending on a large number of factors, and may range anywhere from a few milliseconds to several seconds. That sounds bad, but let’s get a little more specific, using AWS Lambda as an example.
Initialization of a Lambda function will either be a “warm start”—reusing an instance of a Lambda function and its host container from a previous event—or a “cold start” —creating a new container instance, starting the function host process, etc. Unsurprisingly, when considering startup latency, it’s these cold starts that bring the most concern.
Cold-start latency depends on many variables: the language you use, how many libraries you’re using, how much code you have, the configuration of the Lambda function environment itself, whether you need to connect to VPC resources, etc. Many of these aspects are under a developer’s control, so it’s often possible to reduce the startup latency incurred as part of a cold start.
Equally as variable as cold-start duration is cold-start frequency. For instance, if a function is processing 10 events per second, with each event taking 50 ms to process, you’ll likely only see a cold start with Lambda every 100,000–200,000 events or so. If, on the other hand, you process an event once per hour, you’ll likely see a cold start for every event, since Amazon retires inactive Lambda instances after a few minutes. Knowing this will help you understand whether cold starts will impact you on aggregate, and whether you might want to perform “keep alives” of your function instances to avoid them being put out to pasture.
Are cold starts a concern? It depends on the style and traffic shape of your application. My former team at Intent Media has an asynchronous message-processing Lambda app implemented in Java (typically the language with the slowest startup time) which processes hundreds of millions of messages per day, and they have no concerns with startup latency for this component. That said, if you were writing a low-latency trading application you probably wouldn’t want to use cloud-hosted FaaS systems at this time, no matter the language you were using for implementation.
Whether or not you think your app may have problems like this, you should test performance with production-like load. If your use case doesn’t work now you may want to try again in a few months, since this is a major area of continual improvement by FaaS vendors.
For much more detail on cold starts, please see my article on the subject.
API gateways
One aspect of Serverless that we brushed upon earlier is an “API gateway.” An API gateway is an HTTP server where routes and endpoints are defined in configuration, and each route is associated with a resource to handle that route. In a Serverless architecture such handlers are often FaaS functions.
When an API gateway receives a request, it finds the routing configuration matching the request, and, in the case of a FaaS-backed route, will call the relevant FaaS function with a representation of the original request. Typically the API gateway will allow mapping from HTTP request parameters to a more concise input for the FaaS function, or will allow the entire HTTP request to be passed through, typically as a JSON object. The FaaS function will execute its logic and return a result to the API gateway, which in turn will transform this result into an HTTP response that it passes back to the original caller.
Amazon Web Services have their own API gateway (slightly confusingly named “API Gateway”), and other vendors offer similar abilities. Amazon’s API Gateway is a BaaS (yes, BaaS!) service in its own right in that it’s an external service that you configure, but do not need to run or provision yourself.
Beyond purely routing requests, API gateways may also perform authentication, input validation, response code mapping, and more. (If your spidey senses are tingling as you consider whether this is actually such a good idea, hold that thought! We'll consider this further later.)
One use case for an API gateway with FaaS functions is creating HTTP-fronted microservices in a Serverless way with all the scaling, management, and other benefits that come from FaaS functions.
When I first wrote this article, the tooling for Amazon’s API Gateway, at least, was achingly immature. Such tools have improved significantly since then. Components like AWS API Gateway are not quite “mainstream,” but hopefully they’re a little less painful than they once were, and will only continue to improve.
Tooling
The comment above about maturity of tooling also applies to Serverless FaaS in general. In 2016 things were pretty rough; by 2018 we’ve seen a marked improvement, and we expect tools to get better still.
A couple of notable examples of good “developer UX” in the FaaS world are worth calling out. First of all is Auth0 Webtask which places significant priority on developer UX in its tooling. Second is Microsoft, with their Azure Functions product. Microsoft has always put Visual Studio, with its tight feedback loops, at the forefront of its developer products, and Azure Functions is no exception. The ability it offers to debug functions locally, given an input from a cloud-triggered event, is quite special.
An area that still needs significant improvement is monitoring. I discuss that later on.
Open source
So far I’ve mostly discussed proprietary vendor products and tools. The majority of Serverless applications make use of such services, but there are open-source projects in this world, too.
The most common uses of open source in Serverless are for FaaS tools and frameworks, especially the popular Serverless Framework, which aims to make working with AWS API Gateway and Lambda easier than using the tools provided by AWS. It also provides an amount of cross-vendor tooling abstraction, which some users find valuable. Examples of similar tools include Claudia and Zappa. Another example is Apex, which is particularly interesting since it allows you to develop Lambda functions in languages other than those directly supported by Amazon.
The big vendors themselves aren’t getting left behind in the open-source tool party though. AWS’s own deployment tool, SAM—the Serverless Application Model—is also open source.
One of the main benefits of proprietary FaaS is not having to be concerned about the underlying compute infrastructure (machines, VMs, even containers). But what if you want to be concerned about such things? Perhaps you have some security needs that can’t be satisfied by a cloud vendor, or maybe you have a few racks of servers that you’ve already bought and don’t want to throw away. Can open source help in these scenarios, allowing you to run your own “Serverful” FaaS platform?
Yes, and there’s been a good amount of activity in this area. One of the initial leaders in open-source FaaS was IBM (with OpenWhisk, now an Apache project) and surprisingly—to me at least!—Microsoft, which open sourced much of its Azure Functions platform. Many other self-hosted FaaS implementations make use of an underlying container platform, frequently Kubernetes, which makes a lot of sense for many reasons. In this arena it’s worth exploring projects like Galactic Fog, Fission, and OpenFaaS. This is a large, fast-moving world, and I recommend looking at the work that the Cloud Native Computing Federation (CNCF) Serverless Working Group have done to track it.
What isn’t Serverless?
So far in this article I've described Serverless as being the union of two ideas: Backend as a Service and Functions as a Service. I've also dug into the capabilities of the latter. For more precision about what I see as the key attributes of a Serverless service (and why I consider even older services like S3 to be Serverless), I refer you to another article of mine: Defining Serverless.
Before we start looking at the very important area of benefits and drawbacks, I'd like to spend one more quick moment on definition. Let’s define what Serverless isn't.
Comparison with PaaS
Given that Serverless FaaS functions are very similar to Twelve-Factor applications, are they just another form of "Platform as a Service" (PaaS) like Heroku? For a brief answer I refer to Adrian Cockcroft
If your PaaS can efficiently start instances in 20ms that run for half a second, then call it serverless.
In other words, most PaaS applications are not geared towards bringing entire applications up and down in response to an event, whereas FaaS platforms do exactly this.
If I’m being a good Twelve-Factor app developer, this doesn’t necessarily impact how I program and architect my applications, but it does make a big difference in how I operate them. Since we're all good DevOps-savvy engineers, we're thinking about operations as much as we’re thinking about development, right?
The key operational difference between FaaS and PaaS is scaling. Generally with a PaaS you still need to think about how to scale—for example, with Heroku, how many Dynos do you want to run? With a FaaS application this is completely transparent. Even if you set up your PaaS application to auto-scale you won’t be doing this to the level of individual requests (unless you have a very specifically shaped traffic profile), so a FaaS application is much more efficient when it comes to costs.
Given this benefit, why would you still use a PaaS? There are several reasons, but tooling is probably the biggest. Also some people use PaaS platforms like Cloud Foundry to provide a common development experience across a hybrid public and private cloud; at time of writing there isn’t a FaaS equivalent as mature as this.
Comparison with containers
One of the reasons to use Serverless FaaS is to avoid having to manage application processes at the operating-system level. PaaS services, like Heroku, also provide this capability, and I’ve described above how PaaS is different to Serverless FaaS. Another popular abstraction of processes are containers, with Docker being the most visible example of such a technology. Container hosting systems such as Mesos and Kubernetes, which abstract individual applications from OS-level deployment, are increasingly popular. Even further along this path we see cloud-hosting container platforms like Amazon ECS and EKS, and Google Container Engine which, like Serverless FaaS, let teams avoid having to manage their own server hosts at all. Given the momentum around containers, is it still worth considering Serverless FaaS?
Principally the argument I made for PaaS still holds with containers - for Serverless FaaS scaling is automatically managed, transparent, and fine grained, and this is tied in with the automatic resource provisioning and allocation I mentioned earlier. Container platforms have traditionally still needed you to manage the size and shape of your clusters.
I’d also argue that container technology is still not mature and stable, although it is getting ever closer to being so. That’s not to say that Serverless FaaS is mature, of course, but picking which rough edges you’d like is still the order of the day.
It’s also important to mention that self-scaling container clusters are now available within container platforms. Kubernetes has this built in with "Horizontal Pod Autoscaling," and services like AWS Fargate also make the promise of “Serverless Containers.”
As we see the gap of management and scaling between Serverless FaaS and hosted containers narrow, the choice between them may just come down to style and type of application. For example, it may be that FaaS is seen as a better choice for an event-driven style with few event types per application component, and containers are seen as a better choice for synchronous-request–driven components with many entry points. I expect in a fairly short period of time that many applications and teams will use both architectural approaches, and it will be fascinating to see patterns of such use emerge.
#NoOps
Serverless doesn’t mean "No Ops"—though it might mean “No sysadmin” depending on how far down the Serverless rabbit hole you go.
“Ops” means a lot more than server administration. It also means—at least—monitoring, deployment, security, networking, support, and often some amount of production debugging and system scaling. These problems all still exist with Serverless apps, and you’re still going to need a strategy to deal with them. In some ways Ops is harder in a Serverless world because a lot of this is so new.
The sysadmin is still happening—you’re just outsourcing it with Serverless. That’s not necessarily a bad (or good) thing—we outsource a lot, and its goodness or badness depends on what precisely you’re trying to do. Either way, at some point the abstraction will likely leak, and you’ll need to know that human sysadmins somewhere are supporting your application.
Charity Majors gave a great talk on this subject at the first Serverlessconf. (You can also read her two write-ups on it: WTF is operations? and Operational Best Practices.)
Stored Procedures as a Service
I wonder if serverless services will become a thing like stored procedures, a good idea that quickly turns into massive technical debt
Another theme I’ve seen is that Serverless FaaS is “Stored Procedures as a Service.” I think that's come from the fact that many examples of FaaS functions (including some I've used in this article) are small pieces of code that are tightly integrated with a database. If that's all we could use FaaS for I think the name would be useful, but because it is really just a subset of FaaS's capability, I don’t think it’s useful to think about FaaS in these terms.
That being said, it’s worth considering whether FaaS comes with some of the same problems of stored procedures, including the technical debt concern Camille mentions in the above-referenced tweet. There are many lessons that come from using stored procedures that are worth reviewing in the context of FaaS and seeing whether they apply. Consider that stored procedures:
- Often require vendor-specific language, or at least vendor-specific frameworks / extensions to a language
- Are hard to test since they need to be executed in the context of a database
- Are tricky to version control or to treat as a first class application
While not all of these will necessarily apply to all implementations of stored procs, they’re certainly problems one might come across. Let’s see if they might apply to FaaS:
(1) is definitely not a concern for the FaaS implementations I’ve seen so far, so we can scrub that one off the list right away.
For (2) since we’re dealing with "just code," unit testing is definitely as easy as any other code. Integration testing is a different (and legitimate) question though, and one which we’ll discuss later.
For (3), again since FaaS functions are “just code” version control is okay. Until recently application packaging was also a concern, but we’re starting to see maturity here, with tools like Amazon’s Serverless Application Model (SAM) and the Serverless Framework that I mentioned earlier. At the beginning of 2018 Amazon even launched a “Serverless Application Repository” (SAR) providing organizations with a way to distribute applications, and application components, built on AWS Serverless services. (Read more on SAR in my fittingly titled article Examining the AWS Serverless Application Repository.)
Benefits
So far I've mostly tried to stick to just defining and explaining what Serverless architectures have come to mean. Now I'm going to discuss some of the benefits and drawbacks to such a way of designing and deploying applications. You should definitely not take any decision to use Serverless without significant consideration and weighing of pros and cons.
Let’s start off in the land of rainbows and unicorns and look at the benefits of Serverless.
Reduced operational cost
Serverless is, at its most simple, an outsourcing solution. It allows you to pay someone to manage servers, databases and even application logic that you might otherwise manage yourself. Since you're using a predefined service that many other people will also be using we see an Economy of Scale effect: you pay less for your managed database because one vendor is running thousands of very similar databases.
The reduced costs appear to you as the total of two aspects. The first are infrastructure cost gains that come purely from sharing infrastructure (e.g., hardware, networking) with other people. The second are labor cost gains: you'll be able to spend less of your own time on an outsourced Serverless system than on an equivalent developed and hosted by yourself.
This benefit, however, isn't too different than what you'll get from Infrastructure as a Service (IaaS) or Platform as a Service (PaaS). But we can extend this benefit in two key ways, one for each of Serverless BaaS and FaaS.
BaaS: reduced development cost
IaaS and PaaS are based on the premise that server and operating system management can be commodified. Serverless Backend as a Service, on the other hand, is a result of entire application components being commodified.
Authentication is a good example. Many applications code their own authentication functionality, which often includes features such as signup, login, password management, and integration with other authentication providers. On the whole this logic is very similar across most applications, and services like Auth0 have been created to allow us to integrate ready-built authentication functionality into our application without us having to develop it ourselves.
On the same thread are BaaS databases, like Firebase's database service. Some mobile application teams have found it makes sense to have the client communicate directly with a server-side database. A BaaS database removes much of the database administration overhead, and typically provides mechanisms to perform appropriate authorization for different types of users, in the patterns expected of a Serverless app.
Depending on your background, these ideas might make you squirm (likely for reasons that we'll get into in the drawbacks section) but there’s no denying the number of successful companies that have been able to produce compelling products with barely any of their own server-side code. Joe Emison gave a couple of examples of this at the first Serverless Conference.
FaaS: scaling costs
One of the joys of Serverless FaaS is that—as I put it earlier in this article—“horizontal scaling is completely automatic, elastic, and managed by the provider.” There are several benefits to this but on the basic infrastructural side the biggest benefit is that you only pay for the compute that you need, down to a 100ms boundary in the case of AWS Lambda. Depending on your traffic scale and shape, this can be a huge economic win for you.
Example: occasional requests
Say you're running a server application that only processes one request every minute, it takes 50 ms to process each request, and your mean CPU usage over an hour is 0.1 percent. If this application is deployed to its own dedicated host then this is wildly inefficient. A thousand other similar applications could all share that one machine.
Serverless FaaS captures this inefficiency, handing the benefit to you in reduced cost. With the example application above you'd be paying for just 100 ms of compute every minute, which is 0.15 percent of the time overall.
This has the following knock-on benefits:
- For would-be microservices that have very small load requirements it gives support to breaking down components by logic/domain even if the operational costs of such fine granularity might have been otherwise prohibitive.
- Such cost benefits are a great democratizer. If companies or teams want to try out something new they have extremely small operational costs associated with “dipping their toe in the water” when they use FaaS for their compute needs. In fact, if your total workload is relatively small (but not entirely insignificant), you may not need to pay for any compute at all due to the “free tier” provided by some FaaS vendors.
Example: inconsistent traffic
Let's look at another example. Say your traffic profile is very spiky—perhaps your baseline traffic is 20 requests per second, but that every five minutes you receive 200 requests per second (10 times the usual number) for 10 seconds. Let's also assume, for the sake of the example, that your baseline performance maxes out your preferred host server type, and that you don't want to reduce your response time during the traffic spike phase. How do you solve for this?
In a traditional environment you may need to increase your total hardware count by a factor of 10 over what it might otherwise be to handle the spikes, even though the total durations of the spikes account for less than 4 percent of total machine uptime. Auto-scaling is likely not a good option here due to how long new instances of servers will take to come up—by the time your new instances have booted the spike phase will be over.
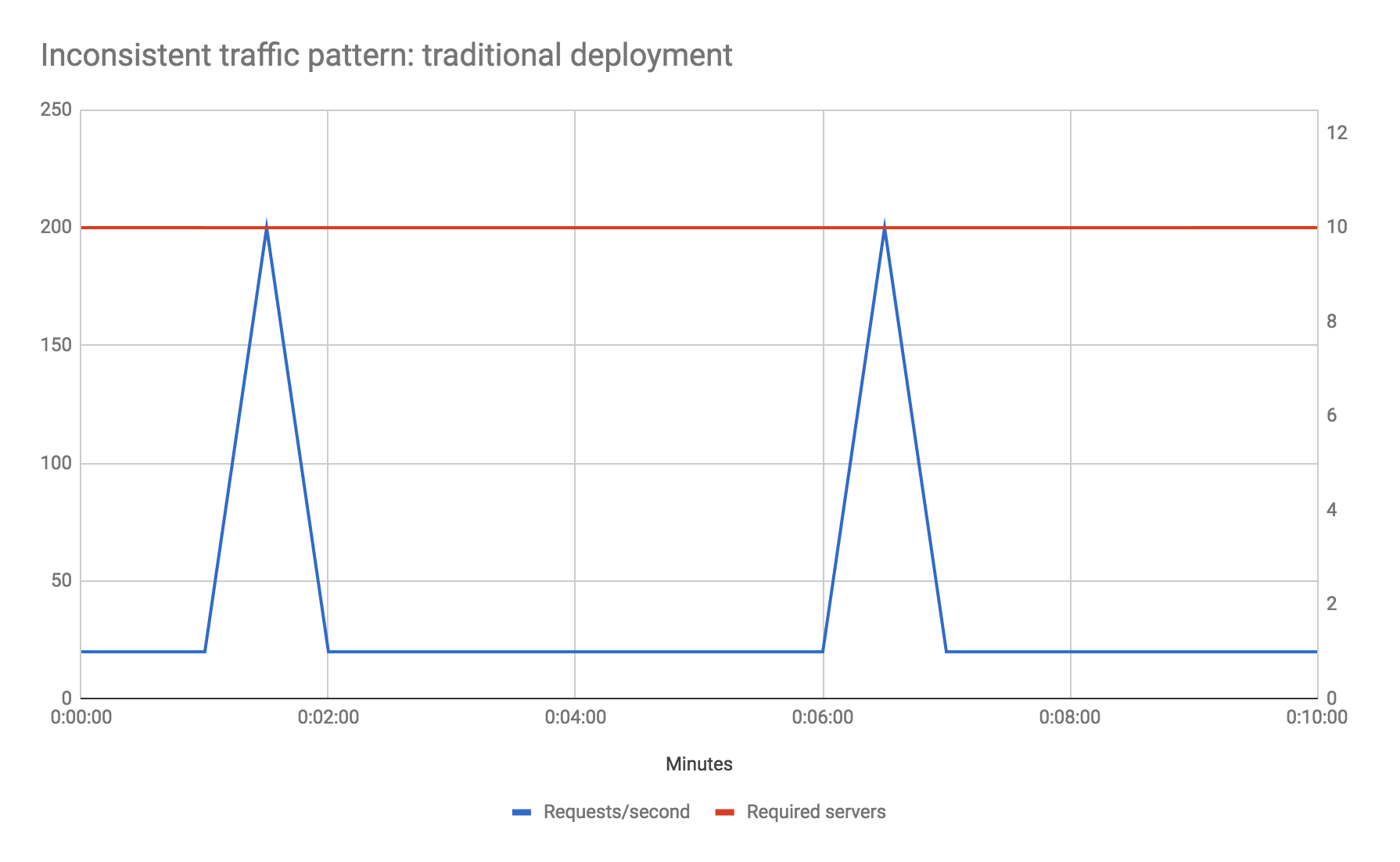
With Serverless FaaS however this becomes a non-issue. You literally do nothing differently than if your traffic profile was uniform, and you only pay for the extra compute capacity during the spike phases.
Obviously I've deliberately picked examples here for which Serverless FaaS gives huge cost savings, but the point is to show that, from a scaling viewpoint, unless you have a very steady traffic shape that consistently uses the whole capacity of your server hosts, then you may save money using FaaS.
One caveat about the above: if your traffic is uniform and would consistently make good utilization of a running server you may not see this cost benefit, and you may actually spend more by using FaaS. You should do some math and compare current provider costs with the equivalents of running full-time servers to see whether costs are acceptable.
For more detail on the cost benefits of FaaS I recommend the paper “Serverless Computing: Economic and Architectural Impact” by Gojko Adzic and Robert Chatley.
Optimization is the root of some cost savings
There is one more interesting aspect to mention about FaaS costs: any performance optimizations you make to your code will not only increase the speed of your app, but they’ll have a direct and immediate link to reduction in operational costs, subject to the granularity of your vendor’s charging scheme. For example, say an application initially takes one second to process an event. If, through code optimization, this is reduced to 200 ms, it will (on AWS Lambda) immediately see an 80 percent savings in compute costs without making any infrastructural changes.
Easier operational management
This next section comes with a giant asterisk—some aspects of operations are still tough for Serverless, but for now we’re sticking with our unicorn and rainbow friends…
On the Serverless BaaS side of the fence, it’s fairly obvious why operational management is more simple than other architectures: supporting fewer components equals less work.
On the FaaS side there are a number of aspects at play though, and I’m going to dig into a couple of them.
Scaling benefits of FaaS beyond infrastructure costs
While scaling is fresh in our minds from the previous section it’s worth noting that not only does the scaling functionality of FaaS reduce compute cost, it also reduces operational management because the scaling is automatic.
In the best case, if your scaling process was a manual one—say, a human being needs to explicitly add and remove instances to an array of servers—with FaaS you can happily forget about that and let your FaaS vendor scale your application for you.
Even if you’ve gotten to the point of using auto-scaling in a non-FaaS architecture, that still requires setup and maintenance. This work is no longer necessary with FaaS.
Similarly, since scaling is performed by the provider on every request/event, you no longer need to think about the question of how many concurrent requests you can handle before running out of memory or seeing too much of a performance hit—at least not within your FaaS-hosted components. Downstream databases and non-FaaS components will have to be reconsidered in light of a possibly significant increase in their load.
Reduced packaging and deployment complexity
Packaging and deploying a FaaS function is simple compared to deploying an entire server. All you’re doing is packaging all your code into a zip file, and uploading it. No Puppet/Chef, no start/stop shell scripts, no decisions about whether to deploy one or many containers on a machine. If you’re just getting started you don’t even need to package anything—you may be able to write your code in the vendor console itself (this, obviously, is not recommended for production code!).
This process doesn't take long to describe, but for some teams this benefit may be absolutely huge: a fully Serverless solution requires zero system administration.
PaaS solutions have similar deployment benefits, but as we saw earlier, when comparing PaaS with FaaS, the scaling advantages are unique to FaaS.
Time to market and continuous experimentation
Easier operational management is a benefit that we as engineers understand, but what does that mean to our businesses?
The obvious reason is cost: less time spent on operations equals fewer people needed for operations, as I’ve already described. But a far more important reason in my mind is time to market. As our teams and products become increasingly geared toward lean and agile processes, we want to continually try new things and rapidly update our existing systems. While simple redeployment in the context of continuous delivery allows rapid iteration of stable projects, having a good new-idea-to-initial-deployment capability allows us to try new experiments with low friction and minimal cost.
The new-idea-to-initial-deployment story for FaaS is often excellent, especially for simple functions triggered by a maturely defined event in the vendor’s ecosystem. For instance, say your organization is already using AWS Kinesis, a Kafka-like messaging system, for broadcasting various types of real-time events through your infrastructure. With AWS Lambda you can develop and deploy a new production event listener against that Kinesis stream in minutes—you could try several different experiments all in one day!
While the cost benefits are the most easily expressed improvements with Serverless, it’s this reduction in lead time that makes me most excited. It can enable a product development mindset of continuous experimentation, and that is a true revolution for how we deliver software in companies.
"Greener" computing?
Over the last couple of decades, there’s been a massive increase in the numbers and sizes of data centers in the world. As well as the physical resources necessary to build these centers, the associated energy requirements are so large that Apple, Google, and the like talk about hosting some of their data centers near sources of renewable energy in order to reduce the fossil-fuel burning impact of such sites that would otherwise be necessary.
Idle, but powered up, servers consume an untoward amount of this energy - and they’re a big part of the reason why we need so many, and bigger data centers:
Typical servers in business and enterprise data centers deliver between 5 and 15 percent of their maximum computing output on average over the course of the year.
-- Forbes
That’s extraordinarily inefficient, and creates a huge environmental impact.
On one hand it’s likely that cloud infrastructure has probably helped reduce this impact already since companies can “buy” more servers on demand, only when they absolutely need them, rather than provisioning all only possibly necessary servers a long time in advance. However one could also argue that the ease of provisioning servers may have made the situation worse if a lot of those servers are being left around without adequate capacity management.
Whether we use a self-hosted server, IaaS, or PaaS infrastructure solution we’re still manually making capacity decisions about our applications that will often last months or years. Typically we are cautious, and rightly so, about managing capacity, and so we over-provision, leading to the inefficiencies just described. With a Serverless approach we no longer make such capacity decisions ourselves—we let the Serverless vendor provision just enough compute capacity for our needs in real time. The vendor can then make their own capacity decisions in aggregate across their customers.
This difference should lead to far more efficient use of resources across data centers, and therefore to reductions in environmental impact compared with traditional capacity management approaches.
Drawbacks
So, dear reader, I hope you enjoyed your time in the land of rainbows, unicorns, and all things shiny and nice, because we’re about to get slapped around the face by the wet fish of reality.
There’s certainly a lot to like about Serverless architectures, but they come with significant trade-offs. Some of these trade-offs are inherent to the concepts; they can’t be entirely fixed by progress, and they’re always going to need to be considered. Others are tied to current implementations; with time we can expect to see these resolved.
Inherent drawbacks
Vendor control
With any outsourcing strategy you are giving up control of some of your system to a third-party vendor. Such lack of control may manifest as system downtime, unexpected limits, cost changes, loss of functionality, forced API upgrades, and more. Charity Majors, who I referenced earlier, explains this problem in much more detail in the Tradeoffs section of this article:
[The Vendor service], if it is smart, will put strong constraints on how you are able to use it, so they are more likely to deliver on their reliability goals. When users have flexibility and options it creates chaos and unreliability. If the platform has to choose between your happiness vs thousands of other customers’ happiness, they will choose the many over the one every time — as they should.
Multitenancy problems
Multitenancy refers to the situation where multiple instances of software for several different customers (or tenants) are run on the same machine, and possibly within the same hosting application. It's a strategy to achieve the economy of scale benefits we mentioned earlier. Service vendors try their darndest to make customers feel that they each are the only ones using their system, and typically good service vendors do a great job of that. But no one’s perfect and sometimes multitenant solutions can have problems with security (one customer being able to see another’s data), robustness (an error in one customer’s software causing a failure in a different customer’s software), and performance (a high-load customer causing another to slow down).
These problems are not unique to Serverless systems—they exist in many other service offerings that use multitenancy. AWS Lambda is now mature enough that we don’t expect to see these kind of problems with it, but you should be on the lookout for such issues with any service that is less mature, whether it’s from AWS or other vendors.
Vendor lock-in
It’s very likely that whatever Serverless features you’re using from one vendor will be implemented differently by another vendor. If you want to switch vendors you’ll almost certainly need to update your operational tools (deployment, monitoring, etc.), you’ll probably need to change your code (e.g., to satisfy a different FaaS interface), and you may even need to change your design or architecture if there are differences to how competing vendor implementations behave.
Even if you manage to easily migrate one part of your ecosystem, you may be more significantly impacted by another architectural component. For instance, say you’re using AWS Lambda to respond to events on an AWS Kinesis message bus. The differences between AWS Lambda, Google Cloud Functions and Microsoft Azure Functions may be relatively small, but you’re still not going to be able to hook up the latter two vendor implementations directly to your AWS Kinesis stream. This means that moving, or porting, your code from one solution to another isn’t going to be possible without also moving other chunks of your infrastructure.
A lot of people are scared by this idea—it’s not a great feeling to know that if your chosen cloud vendor today needs to change tomorrow that you have a lot of work to do. Because of this some people adopt a “multi-cloud” approach, developing and operating applications in a way that’s agnostic of the actual cloud vendor being used. Often this is even more costly than a single-cloud approach—so while vendor lock-in is a legitimate concern, I still recommend picking a vendor that you’re happy with and exploiting their capabilities as much as possible. I talk more about why that is in this article.
Security concerns
Embracing a Serverless approach opens you up to a large number of security questions. Here’s just a very brief smattering of things to consider—be sure to explore what else could impact you.
- Each Serverless vendor that you use increases the number of different security implementations embraced by your ecosystem. This increases your surface area for malicious intent and ups the likelihood of a successful attack.
- If using a BaaS database directly from your mobile platforms you are losing the protective barrier a server-side application provides in a traditional application. While this is not a dealbreaker, it does require significant care in designing and developing your application.
- As your organization embraces FaaS you may experience a cambrian explosion of FaaS functions across your company. Each of those functions offers another vector for problems. For instance, in AWS Lambda, every Lambda function typically goes hand in hand with a configured IAM policy, which are easy to get wrong. This is not a simple topic, nor is it one that can be ignored. IAM management needs careful consideration, at least within production AWS accounts.
Repetition of logic across client platforms
With a “full” BaaS architecture no custom logic is written on the server side—it’s all in the client. This may be fine for your first client platform, but as soon as you need your next platform you’re going to need to repeat the implementation of a subset of that logic—and you wouldn’t have needed this repetition in a more traditional architecture. For instance, if using a BaaS database in this kind of system, all your client apps (perhaps web, native iOS, and native Android) now need to be able to communicate with your vendor database, and will need to understand how to map from your database schema to application logic.
Furthermore, if you want to migrate to a new database at any point, you’re going to need to replicate that coding/coordination change across all your different clients.
Loss of server optimizations
With a full BaaS architecture there is no opportunity to optimize your server design for client performance. The ‘Backend For Frontend’ pattern exists to abstract certain underlying aspects of your whole system within the server, partly so that the client can perform operations more quickly and use less battery power in the case of mobile applications. Such a pattern is not available for full BaaS.
Both this and the previous drawback exist for full BaaS architectures where all custom logic is in the client and the only backend services are vendor supplied. A mitigation of both of these is to embrace FaaS, or some other kind of lightweight server-side pattern, to move certain logic to the server.
No in-server state for Serverless FaaS
After a couple of BaaS-specific drawbacks, let’s talk about FaaS for a moment. I said earlier:
FaaS functions have significant restrictions when it comes to local .. state. .. You should not assume that state from one invocation of a function will be available to another invocation of the same function.
The reason for this assumption is that with FaaS we typically have no control over when the host containers for our functions start and stop.
I also said earlier that the alternative to local state was to follow factor number 6 of the Twelve-Factor app, which is to embrace this very constraint:
Twelve-factor processes are stateless and share-nothing. Any data that needs to persist must be stored in a stateful backing service, typically a database.
Heroku recommends this way of thinking, but you can bend the rules when running on their PaaS since you have control of when Heroku Dynos are started and stopped. With FaaS there’s no bending the rules.
So where does your state go with FaaS if you can’t keep it in memory? The quote above refers to using a database, and in many cases a fast NoSQL database, out-of-process cache (e.g., Redis), or an external object/file store (e.g., S3) will be some of your options. But these are all a lot slower than in-memory or on-machine persistence. You’ll need to consider whether your application is a good fit for this.
Another concern in this regard is in-memory caches. Many apps that are reading from a large data set stored externally will keep an in-memory cache of part of that data set. You may be reading from “reference data” tables in a database and using something like Ehcache. Alternatively you may be reading from an HTTP service that specifies cache headers, in which case your in-memory HTTP client can provide a local cache.
FaaS does allow some use of local cache, and this may be useful assuming your functions are used frequently enough. For instance, with AWS Lambda we typically expect a function instance to stick around for a few hours as long as it’s used at least once every few minutes. That means we can use the (configurable) 3 GB RAM, or 512 MB local “/tmp” space, that Lambda can provide us. For some caches this may be sufficient. Otherwise you will need to no longer assume in-process cache, and you’ll need to use a low-latency external cache like Redis or Memcached. However this requires extra work, and may be prohibitively slow depending on your use case.
Implementation drawbacks
The previously described drawbacks are likely always going to exist with Serverless. We’ll see improvements in mitigating solutions, but they’re always going to be there.
The remaining drawbacks, however, come down purely to the current state of the art. With inclination and investment on the part of vendors and/or a heroic community these can all be wiped out. In fact this list has shrunk since the first version of this article.
Configuration
When I wrote the first version of this article AWS offered very little in the way of configuration for Lambda functions. I’m glad to say that has now been fixed, but it’s still something that’s worth checking if you use a less mature platform.
DoS yourself
Here’s an example of why caveat emptor is a key phrase whenever you’re dealing with FaaS. AWS Lambda limits how many concurrent executions of your Lambda functions you can be running at a given time. Say that this limit is one thousand; that means that at any time you are allowed to be executing one thousand function instances. If you to need to go above that you may start getting exceptions, queueing, and/or general slow down.
The problem here is that this limit is across an entire AWS account. Some organizations use the same AWS account for both production and testing. That means if someone, somewhere, in your organization performs a new type of load test and starts trying to execute one thousand concurrent Lambda functions, you’ll accidentally DoS your production applications. Oops.
Even if you use different AWS accounts for production and development, one overloaded production lambda (e.g., processing a batch upload from a customer) could cause your separate real-time lambda-backed production API to become unresponsive.
Amazon provides some protection here, by way of reserved concurrency. Reserved concurrency allows you to limit the concurrency of a Lambda function so that it doesn’t blow up the rest of your account, while simultaneously making sure there is always capacity available no matter what the other functions in an account are doing. However, reserved concurrency is not turned on by default for an account, and it needs careful management.
Execution duration
Earlier in the article I mentioned that AWS Lambda functions are aborted if they run for longer than five minutes. This has been consistent now for a couple of years, and AWS has shown no signs of changing it.
Startup latency
I talked about cold starts earlier, and mentioned my article on the subject. AWS has improved this area over time, but there are still significant concerns here, especially for only occasionally triggered JVM-implemented functions and/or functions that need access to VPC resources. Continued improvements are expected in this area.
Okay, that’s enough picking on AWS Lambda specifically. I’m sure other vendors also have some pretty ugly skeletons barely in their closets.
Testing
Unit testing Serverless apps is fairly simple for reasons I’ve talked about earlier: any code that you write is “just code,” and for the most part there aren’t a whole bunch of custom libraries you have to use or interfaces that you have to implement.
Integration testing Serverless apps, on the other hand, is hard. In the BaaS world you’re deliberately relying on externally provided systems rather than, for instance, your own database. So should your integration tests use the external systems too? If yes, then how amenable are those systems to testing scenarios? Can you easily tear up and tear down state? Can your vendor give you a different billing strategy for load testing?
If you want to stub those external systems for integration testing does the vendor provide a local stub simulation? If so, how good is the fidelity of the stub? If the vendor doesn’t supply a stub how will you implement one yourself?
The same kinds of problems exist in FaaS land, although there’s been improvement in this area. It’s now possible to run FaaS functions locally for both Lambda and Microsoft Azure. However no local environment can fully simulate the cloud environment; relying solely on local FaaS environments is not a strategy I’d recommend. In fact, I’d go further and suggest that your canonical environment for running automated integration tests, at least as part of a deployment pipeline, should be the cloud, and that you should use the local testing environments primarily for interactive development and debugging. These local testing environments continue to improve - SAM CLI, for example, provides fast feedback for developing a Lambda-backed HTTP API application.
And remember those cross-account execution limits I mentioned a couple of sections ago when running integration tests in the cloud? You probably want to at least isolate such tests from your production cloud accounts, and likely use even more fine-grained accounts than that.
Part of the reason that considering integration tests is a big deal is that our units of integration with Serverless FaaS (i.e., each function) are a lot smaller than with other architectures, so we rely on integration testing a lot more than we may with other architectural styles.
Relying on cloud-based testing environments rather than running everything locally on my laptop has been quite a shock to me. But times change, and the capabilities we get from the cloud are similar to what engineers at Google and the like have had for over a decade. Amazon now even lets you run your IDE in the cloud. I haven’t quite made that jump yet—but it’s probably coming.
Debugging
Debugging with FaaS is an interesting area. There’s been progress here, mostly related to running FaaS functions locally, in line with the testing updates discussed above. Microsoft, as I mentioned earlier, provides excellent debugging support for functions run locally, yet triggered by remote events. Amazon offers something similar, but not yet triggered by production events.
Debugging functions actually running in a production cloud environment is a different story. Lambda at least has no support for that yet, though it would be great to see such a capability.
Deployment, packaging, and versioning
This is an area under active improvement. AWS has made vast strides in improving this area, and I discuss it further in the “Future of Serverless” section a little later.
Discovery
“Discovery” is a frequently discussed topic in the microservices world: it’s the question of how one service can call the correct version of another service. In the Serverless world there’s been little discussion of discovery. Initially this concerned me, but now I’m less worried. Many usages of Serverless are inherently event driven, and here the consumer of an event typically self registers to some extent. For API-oriented usages of FaaS, we typically use them behind an API gateway. In this context we use DNS in front of the API gateway, and automated deployment/traffic shifting behind the gateway. We may even use further layers in front of the API gateway (e.g., using AWS CloudFront) to support cross-region resiliency.
I’m leaving this idea in “limitations” since I don’t think it’s been proven yet, but it may end up being fine after all.
Monitoring and observability
Monitoring is a tricky area for FaaS because of the ephemeral nature of containers. Most of the cloud vendors give you some amount of monitoring support, and we’ve seen a lot of third-party work here from traditional monitoring vendors too. Still, whatever they—and you—can ultimately do depends on the fundamental data the vendor gives you. This may be fine in some cases, but for AWS Lambda, at least, it is very basic. What we really need in this area are open APIs and the ability for third-party services to help out more.
API gateway definition, and over-ambitious API gateways
Thoughtworks, as part of its Technology Radar publication, has discussed over-ambitious API gateways. While the link refers to API gateways in general (e.g., for those fronting traditionally deployed microservices) it can definitely apply to the use of API gateways as HTTP frontend-to-FaaS functions. The problem is that API gateways offer the opportunity to perform much application-specific logic within their own configuration/definition domain. This logic is typically hard to test, version control, and, sometimes, define. Typically it’s far better for such logic to remain in program code like the rest of the application.
There’s definitely a tension here though. If we consider an API gateway as a BaaS, isn’t it valuable to consider all the options it gives us, in order to save ourselves work? And if we’re paying for use of an API gateway per request, as opposed to by per CPU utilization, isn’t it more cost efficient to maximize the use of the API gateway’s functionality?
My guidance is to use enhanced API gateway functionality judiciously, and only if it really is saving you effort in the long run, including in how it is deployed, monitored, and tested. Definitely don’t use API gateway features that can’t be expressed within a source-controllable configuration file or deployment script.
Regarding difficulty of definition, Amazon’s API gateway used to force you to create some tricky configuration to map HTTP requests and responses to/from Lambda functions. Much of that has been made more simple with Lambda proxy integration, but you still need to understand some occasionally tricky nuances. Those elements themselves are made easier using open-source projects like the Serverless Framework and Claudia.js, or Amazon’s Serverless Application Model.
Deferring of operations
I mentioned earlier that Serverless is not “No Ops”—there’s still plenty to do from monitoring, architectural scaling, security, and networking points of view. However, it’s easy to ignore operations when you’re getting started (“Look, ma, no operating system!”). The danger here is getting lulled into a false sense of security. Maybe you have your app up and running but it unexpectedly appears on Hacker News, and suddenly you have 10 times the amount of traffic to deal with and oops! You’re accidentally DoS’ed and have no idea how to deal with it.
The fix here is education. Teams using Serverless systems need to consider operational activities early, and it is on vendors and the community to provide the teaching to help them understand what this means. Areas like preemptive load testing, and chaos engineering, will also help teams teach themselves.
The Future of Serverless
We’re coming to the end of this journey into the world of Serverless architectures. To close out I’m going to discuss a few areas where I think the Serverless world may develop in the coming months and years.
Mitigating the drawbacks
Serverless is still a fairly new world. As such, the previous section on drawbacks was extensive, and I didn’t even cover everything I could have. The most important developments of Serverless are going to be to mitigate the inherent drawbacks and remove, or at least improve, the implementation drawbacks.
Tooling
Tooling continues to be a concern with Serverless, and that’s because so many of the technologies and techniques are new. Deployment/application bundling and configuration have both improved over the last two years, with the Serverless framework and Amazon’s Serverless Application Model leading the way. However the “first 10 minutes” experience still isn’t as universally amazing as it could be, although Amazon and Google could look to Microsoft and Auth0 for more inspiration.
An area I’ve been excited to see being actively addressed by cloud vendors is higher-level release approaches. In traditional systems, teams have typically needed to code their own processes to handle “traffic-shifting” ideas like blue-green deployment and canary releases. With this in mind Amazon supports automatic traffic shifting for both Lambda and API Gateway. Such concepts are even more useful in Serverless systems where so many individually deployed components make up a system—atomic release of 100 Lambda functions at a time is simply not possible. In fact, Nat Pryce described to me the idea for a “mixing desk” approach, one where we can gradually bring groups of components in and out of a traffic flow.
Distributed monitoring is probably the area in need of the most significant improvement. We’ve seen the early days of work here from Amazon’s X-Ray and various third-party products, but this is definitely not a solved problem.
Remote debugging is also something I’d like to see more widespread. Microsoft Azure Functions supports this, but Lambda does not. Being able to breakpoint a remotely running function is a very powerful capability.
Finally, I expect to see improvements for tooling of “meta operations”—how to more effectively look after hundreds or thousands of FaaS functions, configured services, etc. For instance, organizations need to be able to see when certain service instances are no longer used (for security purposes, if nothing else), they need better grouping and visibility of cross-service costs (especially for autonomous teams that have cost responsibilities), and more.
State management
The lack of persistent in-server state for FaaS is fine for a good number of applications, but it’s a deal breaker for many others—whether it be for large cache sets or fast access to session state.
One workaround for high-throughput applications will likely be for vendors to keep function instances alive for longer between events, and let regular in-process caching approaches do their job. This won’t work 100 percent of the time since the cache won’t be warm for every event, but this is the same concern that already exists for traditionally deployed apps using auto-scaling.
A better solution could be very low-latency access to out-of-process data, like being able to query a Redis database with very low network overhead. This doesn’t seem too much of a stretch given that Amazon already offer a hosted Redis solution in their Elasticache product, and that they already allow relative co-location of EC2 (server) instances using Placement Groups.
More likely, though, I think we’re going to see different kinds of hybrid (Serverless and non-Serverless) application architectures embraced to take account of the externalized-state constraint. For instance, for low-latency applications you may see an approach of a regular, long-running server handling an initial request, gathering all the context necessary to process that request from its local and external state, then handing off a fully contextualized request to a farm of FaaS functions that don’t need to look up data externally.
Platform improvements
Certain drawbacks to Serverless FaaS right now come down to the way platforms are implemented. Execution duration, startup latency, and cross-function limits are three obvious ones. These will likely either be fixed by new solutions or given workarounds with possible extra costs. For instance, I imagine that startup latency could be mitigated by allowing a customer to request that two instances of a FaaS function are always available at low latency, with the customer paying for this availability. Microsoft Azure Functions has elements of this idea with Durable Functions, and App Service plan-hosted functions.
Of course we’ll see platform improvements beyond just fixing current deficiencies, and these will be exciting too.
Education
Many vendor-specific inherent drawbacks with Serverless are being mitigated through education. Everyone using such platforms needs to think actively about what it means to have so much of their ecosystems hosted by one or many application vendors. We need to think about questions like, “Do we want to consider parallel solutions from different vendors in case one becomes unavailable?” and “How do applications gracefully degrade in the case of a partial outage?”
Another area for education is technical operations. Many teams now have fewer sysadmins than they used to, and Serverless is going to accelerate this change. But sysadmins do more than just configure Unix boxes and Chef scripts—they’re often the people on the front line of support, networking, security, and the like.
A true DevOps culture becomes even more important in a Serverless world since those other non-sysadmin activities still need to get done, and often it’s developers who are now responsible for them. These activities may not come naturally to many developers and technical leads, so education and close collaboration with operations folk is of utmost importance.
Increased transparency and clearer expectations from vendors
Finally, on the subject of mitigation: vendors are going to have to be even more clear in the expectations we can have of their platforms as we rely on them for more of our hosting capabilities. While migrating platforms is hard, it’s not impossible, and untrustworthy vendors will see their customers taking their business elsewhere.
The emergence of patterns
Our understanding of how and when to use Serverless architectures is still in its infancy. Right now teams are throwing all kinds of ideas at Serverless platforms and seeing what sticks. Thank goodness for pioneers! We’re starting to see patterns of recommended practice occur, and this knowledge will only grow.
Some of the patterns we’re seeing are in application architecture. For instance, how big can FaaS functions get before they get unwieldy? Assuming we can atomically deploy a group of FaaS functions, what are good ways of creating such groupings? Do they map closely to how we’d currently clump logic into microservices, or does the difference in architecture push us in a different direction?
One particularly interesting area of active discussion in Serverless application architecture is how it interacts with event-thinking. Ajay Nair, head of product for AWS Lambda, gave a great talk on this in 2017, and it’s one of the main areas of discussion for the CNCF Serverless Working Group.
Extending this further, what are good ways of creating hybrid architectures between FaaS and traditional “always on” persistent server components? What are good ways of introducing BaaS into an existing ecosystem? And, for the reverse, what are the warning signs that a fully or mostly BaaS system needs to start embracing or using more custom server-side code?
We’re also seeing many more usage patterns discussed. One of the standard examples for FaaS is media conversion, e.g. whenever a large media file is stored to an S3 bucket then automatically running a process to create smaller versions in another bucket. However we also now see significant use of Serverless in data-processing pipelines, highly scalable web APIs, and as general purpose “glue” code in operations. Some of these patterns can be implemented as generic components, directly deployable into organizations; I’ve written about Amazon’s Serverless Application Repository, which has an early form of this idea.
Finally, we’re starting to see recommended operational patterns as tooling improves. How do we logically aggregate logging for a hybrid architecture of FaaS, BaaS, and traditional servers? How do we most effectively debug FaaS functions? A lot of the answers to these questions—and the emerging patterns—are coming from the cloud vendors themselves, and I expect activity to grow in this area.
Globally distributed architectures
In the Pet Store example that I gave earlier we saw that the single Pet Store server was broken up into several server-side components and some logic that moved all the way up to the client—but fundamentally this was still an architecture focused either on the client, or on remote services in known locations.
What we’re starting to see in the Serverless world now is a much fuzzier distribution of responsibility. An example is Amazon’s Lambda@Edge product: a way to run Lambda functions in Amazon’s CloudFront Content Delivery Network. With Lambda@Edge a Lambda function is now globally distributed—a single upload activity by an engineer will mean that function is deployed to over 100 data centers across the globe. This is not a design that we are accustomed to, and comes with a raft of both constraints and capabilities.
Further, Lambda functions can be run on devices, machine-learning models can be run on mobile clients, and before you know it, the bifurcation of “client side” and “server side” no longer seems to make sense. We in fact now see a spectrum of locality of components, spreading out from the human user. Serverless will become Regionless.
Beyond "FaaSification"
Most usages of FaaS that I’ve seen so far are mostly about taking existing code and design ideas and “FaaSifying” them: converting them to a set of stateless functions. This is powerful, but I expect that we’ll start to see more abstractions, and possibly languages, using FaaS as an underlying implementation that gives developers the benefits of FaaS without actually thinking about their application as a set of discrete functions.
As an example, I don’t know whether Google uses a FaaS implementation for its Dataflow product, but I can imagine someone creating a product or open-source project that does something similar, and using FaaS as an implementation. A comparison here is something like Apache Spark . Spark is a tool for large-scale data processing, and offers very high-level abstractions that can use Amazon EMR and Hadoop as its underlying platform.
Testing
I think there’s more work to be done on integration and acceptance testing of Serverless systems, but a lot of this work is the same as “cloud native” microservice systems developed in more traditional ways.
One radical idea here is to embrace ideas like testing in production and monitoring-driven development; once code has passed basic unit-test validation, deploy to a subset of traffic and see how it compares to the previous version. This can be combined with the traffic-shifting tools I mentioned earlier. This doesn’t work for all contexts, but it can be a surprisingly effective tool for many teams.
Portable implementations
There are a couple ways that teams can use Serverless, while being less tied to specific cloud vendors.
Abstractions over vendor implementations
The Serverless Framework primarily exists to ease operational tasks for Serverless applications, but also provides an amount of neutrality about where and how such applications are deployed. For example, it would be great to be able to easily switch, even right now, between AWS API Gateway + Lambda and Auth0 webtask, depending on the operational capabilities of each of the platforms.
A tricky aspect of this is modeling abstracted FaaS coding interfaces without some idea of standardization, but that is precisely the work of the CNCF Serverless Working Group on CloudEvents.
It’s questionable how much value exists in providing a deployment abstraction for multiple platforms though, once complexities of operations rear their ugly heads. For instance getting security right for one cloud is always likely to be different in another cloud.
Deployable implementations
It may sound odd to suggest that we use Serverless techniques without using third-party providers, but consider these thoughts:
- Maybe we’re a large technical organization and we want to start offering a Firebase-like database experience to all of our mobile application development teams, but we want to use our existing database architecture as the back end.
- I talked earlier about “Serverful” FaaS platform—being able to use FaaS-style architecture for some of our projects, but submitting to compliance, legal, etc. reasons to run our applications on premise.
In either of these cases there are still many benefits of using a Serverless approach without those that come from vendor hosting. There’s a precedent here—consider Platform as a Service (PaaS). The initial popular PaaS were all cloud based (e.g., Heroku), but, fairly quickly, people saw the benefits of running a PaaS environment on their own systems—a so-called “Private” PaaS (e.g., Cloud Foundry, as I mentioned earlier in the article).
I can imagine, like private PaaS implementations, that we’ll see both open-source and commercial implementations of BaaS and FaaS concepts becoming popular, especially those integrated with container platforms like Kubernetes.
Community
There is already a good-size Serverless community with multiple conferences, meetups in many cities, and various online groups. I expect this will continue to grow, probably in the same vein of communities like Docker and Spring.
Conclusion
Serverless, despite the confusing name, is a style of architecture where we rely on running our own server-side systems as part of our applications to a smaller extent than usual. We do this through two techniques: BaaS, where we tightly integrate third-party remote application services directly into the frontend of our apps, and FaaS, which moves server-side code from long-running components to ephemeral function instances.
Serverless is not the correct approach for every problem, so be wary of anyone who says it will replace all of your existing architectures. Be careful if you take the plunge into Serverless systems now, especially in the FaaS realm. While there are riches—of scaling and saved deployment effort—to be plundered, there also be dragons—of debugging and monitoring—lurking right around the next corner.
Those riches shouldn’t be dismissed too quickly, however, since there are significant positive aspects to Serverless architecture, including reduced operational and development costs, easier operational management, and reduced environmental impact. But I think the most important benefit is the reduced feedback loop of creating new application components. I’m a huge fan of “lean” approaches, largely because I think there is a lot of value in getting technology in front of an end user as soon as possible to get early feedback, and the reduced time to market that comes with Serverless fits right in with this philosophy.
Serverless services, and our understanding of how to use them, are today (May 2018) in the “slightly awkward teenage years” of maturity. There will be many advances in the field over the coming years, and it will be fascinating to see how Serverless fits into our architectural toolkit.
Acknowledgements
Thanks to the following for their input into this article: Obie Fernandez, Martin Fowler, Paul Hammant, Badri Janakiraman, Kief Morris, Nat Pryce, Ben Rady, Carlos Nunez, John Chapin, Robert Bagge, Karel Sague Alfonso, Premanand Chandrasekaran, Augusto Marietti, Roberto Sarrionandia, Donna Malayeri.
Thanks to Badri Janakiraman and Ant Stanley who provided input for the sidebar on origins of the term.
Thanks to members of my former team at Intent Media for tackling this new technology with appropriately sceptical enthusiasm: John Chapin, Pete Gieser, Sebastián Rojas and Philippe René.
Thanks to Sid Orlando for performing copy-editing.
Finally, thanks to my friends and colleagues in the Serverless community, especially those whose content I link to in this article.
Significant Revisions
22 May 2018: Substantive update of entire article. Read here for details of this update.
04 August 2016: Added “Future” and “Conclusion”
25 July 2016: Added origins sidebar and section “Comparison with containers”
18 July 2016: Added “Drawbacks”
13 July 2016: Added “Benefits”
17 June 2016: Added “What isn’t Serverless’”
16 June 2016: Added “Unpacking ‘Function as a Service’”
15 June 2016: Published first installment - A couple of examples

